Приближенный метод оценки колеблемости вариационного ряда - определение лимита и амплитуды, однако не учитывают значений вариант внутри ряда. Основной общепринятой мерой колеблемости количественного приз­нака в пределах вариационного ряда является среднее квадратичес­кое отклонение (σ - сигма) . Чем больше среднее квадратическое отклонение, тем степень ко­леблемости данного ряда выше.

Методика расчета среднего квадратического отклонения включает следующие этапы:

1. Находят среднюю арифметическую величину (Μ).

2. Определяют отклонения отдельных вариант от средней арифмети­ческой (d=V-M). В медицинской статистике отклонения от средней обозначаются как d (deviate). Сумма всех от­клонений равняется нулю.

3. Возводят каждое отклонение в квадрат d 2 .

4. Перемножают квадраты отклонений на соответствующие частоты d 2 *p.

5. Находят сумму произведений å(d 2 *p)

6. Вычисляют среднее квадратическое отклонение по формуле:

При n больше 30,или при n меньше либо равно 30, где n - число всех вариант.

Значение среднего квадратичного отклонения:

1. Среднее квадратическое отклонение характеризует разброс вариант относительно средней величины (т.е. колеблемость вариационного ряда). Чем больше сигма, тем степень разнообразия данного ряда выше.

2. Среднее квадратичное отклонение используется для сравнительной оценки степени соответствия средней арифметической величины тому вариационному ряду, для которого она вычислена.

Вариации массовых явлений подчиняются закону нормального распределения. Кривая, отображающая это распределение, имеет вид плавной колоколообразной симметричной кривой (кривая Гаусса). Согласно теории вероятности в явлениях, подчиняющихся закону нормального распределения, между значениями средней арифметической и среднего квадратического отклонения существует строгая математическая зависимость. Теоретическое распределение вариант в однородном вариационном ряду подчиняется правилу трех сигм.

Если в системе прямоугольных координат на оси абсцисс отложить значения количественного признака (варианты), а на оси ординат - частоты встречаемости вариант в вариационном ряду, то по сторонам от средней арифметической равномерно располагаются варианты с большими и меньшими значениями.

Установлено, что при нормальном распределении признака:

68,3% значений вариант находится в пределах М±1s

95,5% значений вариант находится в пределах М±2s

99,7% значений вариант находится в пределах М±3s

3. Среднее квадратическое отлонение позволяет установить значения нормы для клинико-биологических показателей. В медицине интервал М±1s обычно принимается за пределы нормы для изучаемого явления. Отклонение оцениваемой величины от средней арифметической больше, чем на 1s указывает на отклонение изучаемого параметра от нормы.

4. В медицине правило трех сигм применяется в педиатрии для индивидуальной оценки уровня физического развития детей (метод сигмальных отклонений), для разработки стандартов детской одежды

5. Среднее квадратическое отклонение необходимо для характеристики степени разнообразия изучаемого признака и вычисления ошибки средней арифметической величины.

Величина среднего квадра­тического отклонения обычно используется для сравнения колеблемости однотипных рядов. Если сравниваются два ряда с разными признаками (рост и масса тела, средняя длительность лечения в стационаре и больничная летальность и т.д.), то непосредственное сопоставление размеров сигм невозможно, т.к. среднеквадратичес­кое отклонение - именованная величина, выраженная в абсолютных числах. В этих случаях применяют коэффициент вариации (Cv) , представляющий собой относительную величину: процентное отноше­ние среднего квадратического отклонения к средней арифметической.

Коэффициент вариации вычисляется по формуле:

Чем выше коэффициент вариации, тем большая изменчивость данно­го ряда. Считают, что коэффициент вариации свыше 30 % свиде­тельствует о качественной неоднородности совокупности.

Определяется как обобщающая характеристика размеров вариации признака в совокупности. Оно равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической, т.е. корень из и может быть найдена так:

1. Для первичного ряда:

2. Для вариационного ряда:

Преобразование формулы среднего квадратичного отклонени приводит ее к виду, более удобному для практических расчетов:

Среднее квадратичное отклонение определяет на сколько в среднем отклоняются конкретные варианты от их среднего значения, и к тому же является абсолютной мерой колеблемости признака и выражается в тех же единицах, что и варианты, и поэтому хорошо интерпретируется.

Примеры нахождения cреднего квадратического отклонения: ,

Для альтернативных признаков формула среднего квадратичного отклонения выглядит так:

где р - доля единиц в совокупности, обладающих определенным признаком;

q - доля единиц, не обладающих этим признаком.

Понятие среднего линейного отклонения

Среднее линейное отклонение определяется как средняя арифметическая абсолютных значений отклонений отдельных вариантов от .

1. Для первичного ряда:

2. Для вариационного ряда:

где сумма n - сумма частот вариационного ряда .

Пример нахождения cреднего линейного отклонения:

Преимущество среднего абсолютного отклонения как меры рассеивания перед размахом вариации, очевидно, так как эта мера основана на учете всех возможных отклонений. Но этот показатель имеет существенные недостатки. Произвольные отбрасывания алгебраических знаков отклонений могут привести к тому, что математические свойства этого показателя являются далеко не элементарными. Это сильно затрудняет использование среднего абсолютного отклонения при решении задач, связанных с вероятностными расчетами.

Поэтому среднее линейное отклонение как мера вариации признака применяется в статистической практике редко, а именно тогда, когда суммирование показателей без учета знаков имеет экономический смысл. С его помощью, например, анализируется оборот внешней торговли, состав работающих, ритмичность производства и т. д.

Среднее квадратическое

Среднее квадратическое применяется , например, для вычисления средней величины сторон n квадратных участков, средних диаметров стволов, труб и т. д. Она подразделяется на два вида.

Средняя квадратичная простая. Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин, то средняя будет являться квадратичной средней величиной.

Она является квадратным корнем из частного от деления суммы квадратов отдельных значений признака на их число:

Средняя квадратичная взвешенная вычисляется по формуле:

где f - признак веса.

Средняя кубическая

Средняя кубическая применяется , например, при определении средней длины стороны и кубов. Она подразделяется на два вида.
Средняя кубическая простая:

При расчете средних величин и дисперсии в интервальных рядах распределения истинные значения признака заменяются центральными значениями интервалов, которые отличны от средней арифметической значений, включенных в интервал. Это приводит к возникновению систематической погрешности при расчете дисперсии. В.Ф. Шеппард определил, что погрешность в расчете дисперсии , вызванная применением сгруппированных данных, составляет 1/12 квадрата величины интервала как в сторону повышения, так и в сторону понижения величины дисперсии.

Поправка Шеппарда должна применяться, если распределение близко к нормальному, относится к признаку с непрерывным характером вариации, построено по значительному количеству исходных данных (n > 500). Однако исходя из того, что в ряде случаев обе погрешности, действуя в разных направлениях компенсируют друг друга, можно иногда отказаться от введения поправок.

Чем меньше значение дисперсии и среднего квадратического отклонения, тем однороднее совокупность и тем более типичной будет средняя величина.
В практике статистики часто возникает необходимость сравнения вариаций различных признаков. Например, большой интерес представляет сравнение вариаций возраста рабочих и их квалификации, стажа работы и размера заработной платы, себестоимости и прибыли, стажа работы и производительности труда и т.д. Для таких сопоставлений показатели абсолютной колеблемости признаков непригодны: нельзя сравнивать колеблемость стажа работы, выраженного в годах, с вариацией заработной платы, выраженной в рублях.

Для осуществления таких сравнений, а также сравнений колеблемости одного и того же признака в нескольких совокупностях с разными средним арифметическим используется относительный показатель вариации - коэффициент вариации.

Структурные средние

Для характеристики центральной тенденции в статистических распределениях не редко рационально вместе со средней арифметической использовать некоторое значение признака X, которое в силу определенных особенностей расположения в ряду распределения может характеризовать его уровень.

Это особенно важно тогда, когда в ряду распределения крайние значения признака имеют нечеткие границы. В связи с этим точное определение средней арифметической, как правило, невозможно, либо очень сложно. В таких случаях средний уровень можно определить, взяв, например, значение признака, которое расположено в середине ряда частот или которое чаще всего встречается в текущем ряду.

Такие значения зависят только от характера частот т. е. от структуры распределения. Они типичны по месту расположения в ряду частот, поэтому такие значения рассматриваются в качестве характеристик центра распределения и поэтому получили определение структурных средних. Они применяются для изучения внутреннего строения и структуры рядов распределения значений признака. К таким показателям относятся .

Среднеквадрати́ческое отклоне́ние (синонимы: среднее квадрати́ческое отклоне́ние , среднеквадрати́чное отклоне́ние , квадрати́чное отклоне́ние ; близкие термины: станда́ртное отклоне́ние , станда́ртный разбро́с ) - в теории вероятностей и статистике наиболее распространённый показатель рассеивания значений случайной величины относительно её математического ожидания . При ограниченных массивах выборок значений вместо математического ожидания используется среднее арифметическое совокупности выборок.

Энциклопедичный YouTube

• 1 / 5

  Среднеквадратическое отклонение измеряется в единицах измерения самой случайной величины и используется при расчёте стандартной ошибки среднего арифметического , при построении доверительных интервалов , при статистической проверке гипотез , при измерении линейной взаимосвязи между случайными величинами. Определяется как квадратный корень из дисперсии случайной величины .

  Среднеквадратическое отклонение:

  s = n n − 1 σ 2 = 1 n − 1 ∑ i = 1 n (x i − x ¯) 2 ; {\displaystyle s={\sqrt {{\frac {n}{n-1}}\sigma ^{2}}}={\sqrt {{\frac {1}{n-1}}\sum _{i=1}^{n}\left(x_{i}-{\bar {x}}\right)^{2}}};}
  • Примечание: Очень часто встречаются разночтения в названиях СКО (Среднеквадратического отклонения) и СТО (Стандартного отклонения) с их формулами. Например, в модуле numPy языка программирования Python функция std() описывается как "standart deviation", в то время как формула отражает СКО (деление на корень из выборки). В Excel же функция СТАНДОТКЛОН() другая (деление на корень из n-1).

  Стандартное отклонение (оценка среднеквадратического отклонения случайной величины x относительно её математического ожидания на основе несмещённой оценки её дисперсии) s {\displaystyle s} :

  σ = 1 n ∑ i = 1 n (x i − x ¯) 2 . {\displaystyle \sigma ={\sqrt {{\frac {1}{n}}\sum _{i=1}^{n}\left(x_{i}-{\bar {x}}\right)^{2}}}.}

  где σ 2 {\displaystyle \sigma ^{2}} - дисперсия ; x i {\displaystyle x_{i}} - i -й элемент выборки; n {\displaystyle n} - объём выборки; - среднее арифметическое выборки:

  x ¯ = 1 n ∑ i = 1 n x i = 1 n (x 1 + … + x n) . {\displaystyle {\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}={\frac {1}{n}}(x_{1}+\ldots +x_{n}).}

  Следует отметить, что обе оценки являются смещёнными. В общем случае несмещённую оценку построить невозможно. Однако оценка на основе оценки несмещённой дисперсии является состоятельной .

  В соответствии с ГОСТ Р 8.736-2011 среднеквадратическое отклонение считается по второй формуле данного раздела. Пожалуйста, сверьте результаты.

  Правило трёх сигм

  Правило трёх сигм ( 3 σ {\displaystyle 3\sigma } ) - практически все значения нормально распределённой случайной величины лежат в интервале (x ¯ − 3 σ ; x ¯ + 3 σ) {\displaystyle \left({\bar {x}}-3\sigma ;{\bar {x}}+3\sigma \right)} . Более строго - приблизительно с вероятностью 0,9973 значение нормально распределённой случайной величины лежит в указанном интервале (при условии, что величина x ¯ {\displaystyle {\bar {x}}} истинная, а не полученная в результате обработки выборки).

  Если же истинная величина x ¯ {\displaystyle {\bar {x}}} неизвестна, то следует пользоваться не σ {\displaystyle \sigma } , а s . Таким образом, правило трёх сигм преобразуется в правило трёх s .

  Интерпретация величины среднеквадратического отклонения

  Большее значение среднеквадратического отклонения показывает больший разброс значений в представленном множестве со средней величиной множества; меньшее значение, соответственно, показывает, что значения в множестве сгруппированы вокруг среднего значения.

  Например, у нас есть три числовых множества: {0, 0, 14, 14}, {0, 6, 8, 14} и {6, 6, 8, 8}. У всех трёх множеств средние значения равны 7, а среднеквадратические отклонения, соответственно, равны 7, 5 и 1. У последнего множества среднеквадратическое отклонение маленькое, так как значения в множестве сгруппированы вокруг среднего значения; у первого множества самое большое значение среднеквадратического отклонения - значения внутри множества сильно расходятся со средним значением.

  В общем смысле среднеквадратическое отклонение можно считать мерой неопределённости. К примеру, в физике среднеквадратическое отклонение используется для определения погрешности серии последовательных измерений какой-либо величины. Это значение очень важно для определения правдоподобности изучаемого явления в сравнении с предсказанным теорией значением: если среднее значение измерений сильно отличается от предсказанных теорией значений (большое значение среднеквадратического отклонения), то полученные значения или метод их получения следует перепроверить. отождествляется с риском портфеля.

  Климат

  Предположим, существуют два города с одинаковой средней максимальной дневной температурой, но один расположен на побережье, а другой на равнине. Известно, что в городах, расположенных на побережье, множество различных максимальных дневных температур меньше, чем у городов, расположенных внутри континента. Поэтому среднеквадратическое отклонение максимальных дневных температур у прибрежного города будет меньше, чем у второго города, несмотря на то, что среднее значение этой величины у них одинаковое, что на практике означает, что вероятность того, что максимальная температура воздуха каждого конкретного дня в году будет сильнее отличаться от среднего значения, выше у города, расположенного внутри континента.

  Спорт

  Предположим, что есть несколько футбольных команд, которые оцениваются по некоторому набору параметров, например, количеству забитых и пропущенных голов, голевых моментов и т. п. Наиболее вероятно, что лучшая в этой группе команда будет иметь лучшие значения по большему количеству параметров. Чем меньше у команды среднеквадратическое отклонение по каждому из представленных параметров, тем предсказуемее является результат команды, такие команды являются сбалансированными. С другой стороны, у команды с большим значением среднеквадратического отклонения сложно предсказать результат, что в свою очередь объясняется дисбалансом, например, сильной защитой, но слабым нападением.

  Использование среднеквадратического отклонения параметров команды позволяет в той или иной мере предсказать результат матча двух команд, оценивая сильные и слабые стороны команд, а значит, и выбираемых способов борьбы.

  $X$. Для начала напомним следующее определение:

  Определение 1

  Генеральная совокупность -- совокупность случайно отобранных объектов данного вида, над которыми проводят наблюдения с целью получения конкретных значений случайной величины, проводимых в неизменных условиях при изучении одной случайной величины данного вида.

  Определение 2

  Генеральная дисперсия -- среднее арифметическое квадратов отклонений значений вариант генеральной совокупности от их среднего значения.

  Пусть значения вариант $x_1,\ x_2,\dots ,x_k$ имеют, соответственно, частоты $n_1,\ n_2,\dots ,n_k$. Тогда генеральная дисперсия вычисляется по формуле:

  Рассмотрим частный случай. Пусть все варианты $x_1,\ x_2,\dots ,x_k$ различны. В этом случае $n_1,\ n_2,\dots ,n_k=1$. Получаем, что в этом случае генеральная дисперсия вычисляется по формуле:

  С этим понятием также связано понятие генерального среднего квадратического отклонения.

  Определение 3

  Генеральное среднее квадратическое отклонение

  \[{\sigma }_г=\sqrt{D_г}\]

  Выборочная дисперсия

  Пусть нам дана выборочная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:

  Определение 4

  Выборочная совокупность -- часть отобранных объектов из генеральной совокупности.

  Определение 5

  Выборочная дисперсия -- среднее арифметическое значений вариант выборочной совокупности.

  Пусть значения вариант $x_1,\ x_2,\dots ,x_k$ имеют, соответственно, частоты $n_1,\ n_2,\dots ,n_k$. Тогда выборочная дисперсия вычисляется по формуле:

  Рассмотрим частный случай. Пусть все варианты $x_1,\ x_2,\dots ,x_k$ различны. В этом случае $n_1,\ n_2,\dots ,n_k=1$. Получаем, что в этом случае выборочная дисперсия вычисляется по формуле:

  С этим понятием также связано понятие выборочного среднего квадратического отклонения.

  Определение 6

  Выборочное среднее квадратическое отклонение -- квадратный корень из генеральной дисперсии:

  \[{\sigma }_в=\sqrt{D_в}\]

  Исправленная дисперсия

  Для нахождения исправленной дисперсии $S^2$ необходимо умножить выборочную дисперсию на дробь $\frac{n}{n-1}$, то есть

  С этим понятием также связано понятие исправленного среднего квадратического отклонения, которое находится по формуле:

  В случае, когда значение вариант не являются дискретными, а представляют из себя интервалы, то в формулах для вычисления генеральной или выборочной дисперсий за значение $x_i$ принимается значение середины интервала, которому принадлежит $x_i.$

  Пример задачи на нахождение дисперсии и среднего квадратического отклонения

  Пример 1

  Выборочная совокупность задана следующей таблицей распределения:

  Рисунок 1.

  Найдем для нее выборочную дисперсию, выборочное среднее квадратическое отклонение, исправленную дисперсию и исправленное среднее квадратическое отклонение.

  Для решения этой задачи для начала сделаем расчетную таблицу:

  

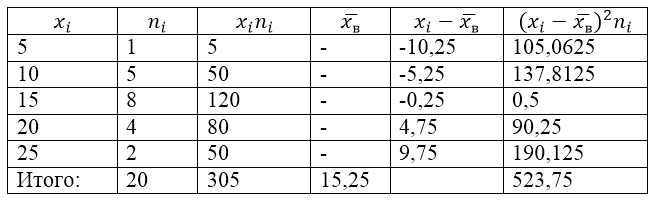
  Рисунок 2.

  Величина $\overline{x_в}$ (среднее выборочное) в таблице находится по формуле:

  \[\overline{x_в}=\frac{\sum\limits^k_{i=1}{x_in_i}}{n}\]

  \[\overline{x_в}=\frac{\sum\limits^k_{i=1}{x_in_i}}{n}=\frac{305}{20}=15,25\]

  Найдем выборочную дисперсию по формуле:

  Выборочное среднее квадратическое отклонение:

  \[{\sigma }_в=\sqrt{D_в}\approx 5,12\]

  Исправленная дисперсия:

  \[{S^2=\frac{n}{n-1}D}_в=\frac{20}{19}\cdot 26,1875\approx 27,57\]

  Исправленное среднее квадратическое отклонение.

  Одним из основных инструментов статистического анализа является расчет среднего квадратичного отклонения. Данный показатель позволяет сделать оценку стандартного отклонения по выборке или по генеральной совокупности. Давайте узнаем, как использовать формулу определения среднеквадратичного отклонения в Excel.

  Сразу определим, что же представляет собой среднеквадратичное отклонение и как выглядит его формула. Эта величина является корнем квадратным из среднего арифметического числа квадратов разности всех величин ряда и их среднего арифметического. Существует тождественное наименование данного показателя — стандартное отклонение. Оба названия полностью равнозначны.

  Но, естественно, что в Экселе пользователю не приходится это высчитывать, так как за него все делает программа. Давайте узнаем, как посчитать стандартное отклонение в Excel.

  Расчет в Excel

  Рассчитать указанную величину в Экселе можно с помощью двух специальных функций СТАНДОТКЛОН.В (по выборочной совокупности) и СТАНДОТКЛОН.Г (по генеральной совокупности). Принцип их действия абсолютно одинаков, но вызвать их можно тремя способами, о которых мы поговорим ниже.

  Способ 1: мастер функций

  
  

  

  Способ 2: вкладка «Формулы»

  
  

  

  Способ 3: ручной ввод формулы

  Существует также способ, при котором вообще не нужно будет вызывать окно аргументов. Для этого следует ввести формулу вручную.

  
  

  

  Как видим, механизм расчета среднеквадратичного отклонения в Excel очень простой. Пользователю нужно только ввести числа из совокупности или ссылки на ячейки, которые их содержат. Все расчеты выполняет сама программа. Намного сложнее осознать, что же собой представляет рассчитываемый показатель и как результаты расчета можно применить на практике. Но постижение этого уже относится больше к сфере статистики, чем к обучению работе с программным обеспечением.